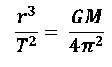Moons of Jupiter

"Mensus eram coelos,
nunc terrae metior umbras,
Mens coelestis erat, corporis umbra iacet."
- Kepler's epitaph
(I measured the skies, now I measure the shadows.
Skybound was the mind, the body rests in the earth.)
Objectives of this lab:
1. Determine the mass of Jupiter.
2. Gain a deeper understanding of Kepler's third law.
3. Learn how to gather and analyze astronomical data.
nunc terrae metior umbras,
Mens coelestis erat, corporis umbra iacet."
- Kepler's epitaph
(I measured the skies, now I measure the shadows.
Skybound was the mind, the body rests in the earth.)
Objectives of this lab:
1. Determine the mass of Jupiter.
2. Gain a deeper understanding of Kepler's third law.
3. Learn how to gather and analyze astronomical data.
Introduction
|
We can deduce some properties of celestial bodies from their motions despite the fact that we cannot directly measure them.
In 1543, Nicolaus Copernicus hypothesized that the planets revolve in circular orbits around the sun. Tycho Brahe (1546-1601) carefully observed the location of the planets and 777 stars over a period of 20 years using a sextant and compass. These observations were used by Johannes Kepler, a student of Brahe's to deduce three emperical mathematical laws governing the orbit of one body around another. Kepler's third law for a moon orbiting a much larger body is C = r^3/T^2, where C is a constant, r is the length of the semi-major axis of the elliptical orbit in units of the mean Earth-Sun distance, 1 A.U. (astro-nomical unit), and T is the planetary orbit in Earth years. If the orbit is circular (as will be assumed in this lab) the semi-major axis is the same as the radius of the orbit. Newton expanded on Kepler’s Third Law, by using his Universal Law of Gravitation to solve for the constant C and derived: where G is the gravitational constant 6.67x10^-11 Nm^2/kg^2 and M is the mass of the larger body.
|
In 1609, the telescope was invented, allowing the observations of objects not visible to the naked eye. Galileo used a telescope to discover that Jupiter had four moons orbiting it and made exhaustive studies of this system. The Jupiter system was especially important because it is a miniature version of the solar system which could be studied in order to understand the motions of the solar system. The Jupiter system provided clear evidence that Copernicus' heliocentric model of the solar system was physically possible. Unfortunately for Galileo, the inquisition took issue with his findings; he was tried and forced to recant.
The purpose of this lab is to observe the motion of the moons of Jupiter and then use Kepler's third law and the expansion to his law offered by Newton’s Universal Law of Gravitation to deduce the mass of Jupiter. The four Galilean moons, Io, Europa, Ganymede and Callisto are easily seen through a small telescope, and the CLEA software will simulate these observations. Useful Links: |
Directions
The CLEA software simulates a telescope allowing you to make your “observations” of these distant celestrial objects. The program has already been downloaded from the CLEA website onto your school laptop (a link is provided on the SHS AP Physics homepage and in the links section above if you'd like to download the software on your home computer). To begin the program, select CLEA_JUP and Login. After entering your names and lab table number, choose the Start option to set the starting date and time. Note that during the lab you may want to go back to this table to reset the “Interval Between Observations.”
Jupiter is in the center of the screen, while the small point-like moons are to either side. Sometimes a moon is behind Jupiter, so it cannot be seen. Even at high magnifications, they are very small compared to Jupiter. The current telescope magnification is displayed at the upper left hand corner of the screen. The date, UT (the time in Greenwich, England) and JD (Julian Date) are displayed in the lower left hand corner of the screen.
Click on each moon, using the highest magnification to get the best position measurement, R, which is recorded in number of “Jupiter Diameters”. R is the distance from the center of Jupiter to the center of the moon. Sometimes a moon will be behind Jupiter, and you will not be able to record data for that moon. To save measurements, simple click record.
You wish to give sufficient time coverage to all four orbits. Since Io's orbital period is significantly shorter than that of Callisto, you will have to change your observation interval to both get good time coverage and to make efficient use of your observing time. You need to cover a full period of the orbit from, for example, the moons most eastern position to its most western position and back.
You should collect approximately 20 days of data, then use the plot function to create r vs. t curves for each moon. The graph is a sine curve whose amplitude is orbital radius and wavelength is period. Now using the orbit of each Galilean moon, determine the quantities that you would have to graph in order to obtain a straight line whose slope will yield the mass of Jupiter. You will have to convert Jupiter Diameters to meters and years to seconds. There are 1.43x10^8 meters in one Jupiter Diameter.
Jupiter is in the center of the screen, while the small point-like moons are to either side. Sometimes a moon is behind Jupiter, so it cannot be seen. Even at high magnifications, they are very small compared to Jupiter. The current telescope magnification is displayed at the upper left hand corner of the screen. The date, UT (the time in Greenwich, England) and JD (Julian Date) are displayed in the lower left hand corner of the screen.
Click on each moon, using the highest magnification to get the best position measurement, R, which is recorded in number of “Jupiter Diameters”. R is the distance from the center of Jupiter to the center of the moon. Sometimes a moon will be behind Jupiter, and you will not be able to record data for that moon. To save measurements, simple click record.
You wish to give sufficient time coverage to all four orbits. Since Io's orbital period is significantly shorter than that of Callisto, you will have to change your observation interval to both get good time coverage and to make efficient use of your observing time. You need to cover a full period of the orbit from, for example, the moons most eastern position to its most western position and back.
You should collect approximately 20 days of data, then use the plot function to create r vs. t curves for each moon. The graph is a sine curve whose amplitude is orbital radius and wavelength is period. Now using the orbit of each Galilean moon, determine the quantities that you would have to graph in order to obtain a straight line whose slope will yield the mass of Jupiter. You will have to convert Jupiter Diameters to meters and years to seconds. There are 1.43x10^8 meters in one Jupiter Diameter.
Concluding Questions
1. Calculate the percentage error with the accepted mass of Jupiter (1.8986 × 10^27 kg).
2. There are moons beyond the orbit of Callisto. Will they have larger or smaller periods than Callisto? Why?
3. Which do you think would cause the larger error in the mass of Jupiter calculation: a ten percent error in "T" or a ten percent error in "r"? Why?
4. Why were Galileo's observations of the orbits of Jupiter's moons an important piece of evidence supporting the heliocentric model of the universe (or, how were they evidence against the contemporary and officially adopted Aristotelian/Roman Catholic, geocentric view)?
2. There are moons beyond the orbit of Callisto. Will they have larger or smaller periods than Callisto? Why?
3. Which do you think would cause the larger error in the mass of Jupiter calculation: a ten percent error in "T" or a ten percent error in "r"? Why?
4. Why were Galileo's observations of the orbits of Jupiter's moons an important piece of evidence supporting the heliocentric model of the universe (or, how were they evidence against the contemporary and officially adopted Aristotelian/Roman Catholic, geocentric view)?
The Lab Report
Please record all work in your lab notebooks organized as follows: Title, Objectives, Background (one paragraph is sufficient), Procedure (you may simply reference this website since the procedure is in the public domain), Data (observation data, period, and orbital radius for each moon), Data Analysis to include all five graphs, slope calculation, and percent error calculation, and Conclusion (addresses the objectives and the concluding questions stated above).
Sample Results
|
| ||||||||||||||||||